Introduction to Intersection Theory
Lecturer: Tahereh Aladpoosh, IPM
Reference: D. Eisenbud, J. Harris, 3264 and All That: A Second Course in Algebraic Geometry, Cambridge University Press, 2016.
Prerequisites: A basic knowledge in classical algebraic geometry; an acquaintance with the language of schemes; an acquaintance with coherent sheaves and their cohomology. (Equivalently, the first 3 chapters of Hartshorne’s Algebraic Geometry).
Date and Time: Wednesdays, 14:00-16:00 Tehran local time, Spring semester 2023.
Location: Hybrid class: in Lecture Hall 2, School of Mathematics; and online (please send an email to taladpoosh@gmail.com to receive the link).
Poster: here
Classes
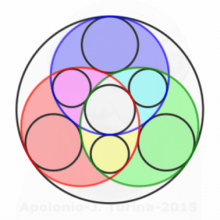
Class 1 (Wed, Bahman 19): welcome, what is the subject, why to study the subject, overview of Intersection Theory and Enumerative Geometry, A historical tour: Apollonius' problem; Bezout's theorem; Steiner's conic problem; Schubert calculus; Hilbert's 15th problem; Fulton and MacPherson's Intersection Theory.
Class 2 (Wed, Bahman 26): cycles, rational equivalence, Chow group for schemes, transversality, Chow ring for smooth varieties, Moving lemma, first main theorem of Intersection Theory.
Class 3 (Wed, Esfand 3): fundamental class, Chow group in some degree, order of zeros and poles, multiplicity along a subvariety, rational equivalence via divisors, Mayer-Vietoris sequence, excision sequence.
Class 4 (Wed, Esfand 10): functoriality of the Chow ring, proper pushforward, flat pullback.
Class 5 (Wed, Farvardin 16): Chow ring of affine space, affine stratification, Chow ring of projective space, class of projective varieties.
Class 6 (Wed, Farvardin 30): generalization of Bezout's theorem, Chow ring of products of projective spaces, class of subvarieties of products, relation with Künneth formula, degree of Veronese varieties.
Class 7 (Wed, Ordibehesht 6): degree of Segre varieties, degree of rational normal scrolls in special cases, class of the diagonal, class of the graph, loci of singular plane cubics.
Class 8 (Wed, Ordibehesht 13): loci of reducible cubics-triangles-asterisks, some enumerative problems, first Chern class of an invertible sheaf, canonical class.
Class 9 (Wed, Ordibehesht 20): adjunction formula, canonical class of hypersurfaces and complete intersections, curves on surfaces, genus formula, self-intersection of a curve on a surface, linked curves in projective 3-space and liaison theory.
Class 10 (Wed, Ordibehesht 27): enumerative problems and enumerative formulas, Chow ring of Grassmannian of lines in projective 3-space, Schuberet classes, how many lines meet 4 general lines, lines meeting a curve, Kleiman's transversality theorem.
Class 11 (Wed, Khordad 3): secant lines to a space curve, how many lines meet 2 general twisted cubic curves twice, static specialization, dynamic specialization.
Class 12 (Wed, Khordad 10): flat limit of intersection cycles, lines lying on a quadric surface, tangent lines to a surface, Grassmannians in general, special Schubert cycles, Young diagram, Pieri's formula, Giambelli's formula.
Class 13 (Wed, Khordad 17): degeneracy locus of a collection of sections of a vector bundle, Chern classes, Whitney's formula, splitting principle, Chow ring of projective bundles, calculating Chern classes for some multilinear functors.
Class 14 (Wed, Khordad 24): Chern classes of varieties, how many lines are contained in a cubic surface, lines on hypersurfaces, Fano schemes and Chern classes, Debarre-de Jong conjecture, Chern character and Todd class, Hirzebruch Riemann-Roch theorem, Grothendieck Riemann-Roch theorem.