Workshop dinner: Wednesday, October 3, 2018 at 19:00
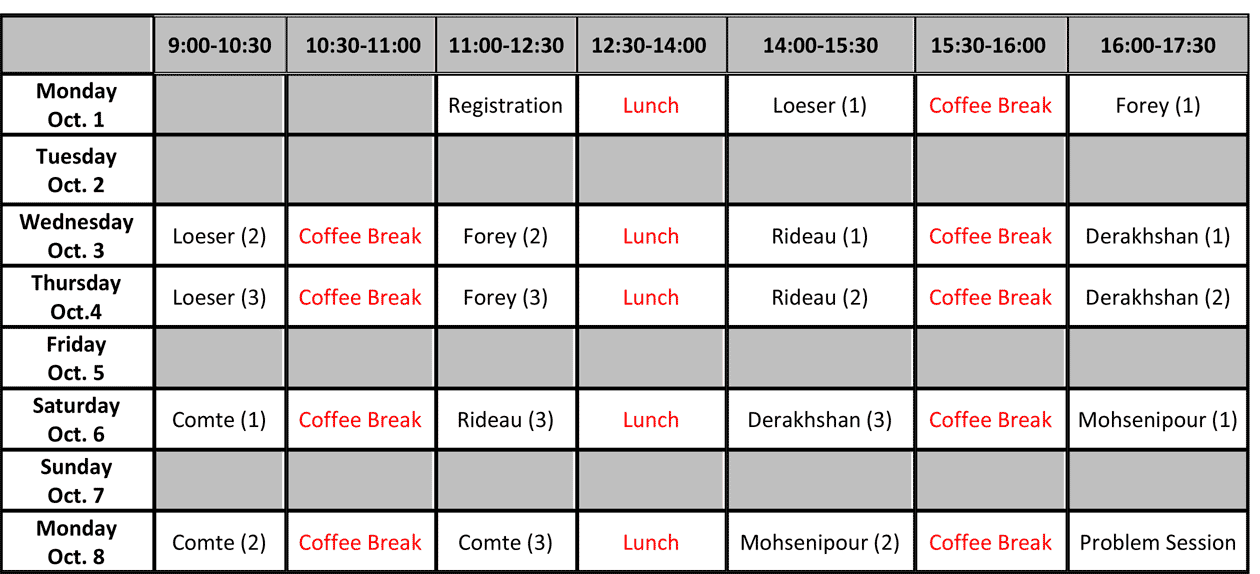
Georges Comte:
Counting rational and algebraic points on real and p-adic tame sets (Abstract)
1) Introduction: the case of curves and zeroes lemmas
2) Pila-Wilkie's result
3) The p-adic case
Jamshid Derakhshan:
Euler products of p-adic integrals (Abstract)
1) Introduction to the main results and applications to global
zeta functions
2) Uniformity in p-adic integrals, definable sets over finite
fields, and abscissa of convergence of Euler products
3) Meromorphic continuation of Euler products, ring of adeles,
and related results and questions
Arthur Forey:
Model theory of the field of p-adic numbers (Abstract) (Notes)
1) Cell decomposition
2) Quantifier elimination and consequences
3) Uniform cell decomposition and the Ax-Kochen-Ershov principle
François Loeser:
Introduction to p-adic numbers and p-adic integrals (Abstract) (Notes)
1) Rationality of generating series via p-adic integration
2) Applications to birational geometry
3) Uniformity patterns for p-adic integrals
Shahram Mohsenipour:
A Logical Diophantine Approach to the Real Algebraic Geometry I, II (Abstract)
Silvain Rideau:
Model theory of algebraically closed valued fields (Abstract) (Notes)
1) Algebra and quantifiers
2) Definable sets and swiss cheeses
3) Imaginaries
